Minimum Spanning Tree를 구현하는 대표적인 방법 중 하나는 Kruskal 알고리즘이다.
Def : Generic MST
어떤 mst의 부분집합 A에 대해서 A 합집합 Edge(u,v) 도 역시 어떤 MST의 부분집합이 될 경우, Edge(u,v)를 안전하다고 한다.
A를 공집합에서 시작하여, 안전한 에지를 A의 원소의 갯수가 n-1이 될 때까지 반복한다.
Th1 : A가 어떤 MST의 부분집합이고, (S,V-S)가 A를 Respect하는 컷 일 때, 이 컷을 Cross하는 에지들 중 가장 작은 가중치의 Edge(u,v)는 A에 대해서 안젆다. 밑에 Kruskal 알고리즘을 설명하며 이를 증명하였다.
Kruskal Algorithm
kruskal 알고리즘은 최소 가중치 순서대로 선택을 한다. 이 때, 선택한 에지가 Cycle을 이루지 않도록 하는 것이 중요하다.
A를 현재까지 선택한 에지의 집합으로 가정할 때, 가장 작은 가중치의 에지를 선택하는 것은 안전하다.
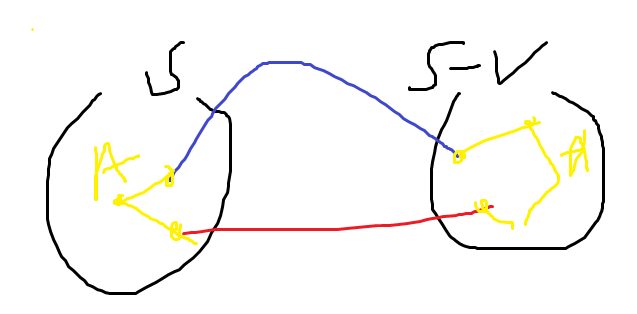
빨간색 선을 가중치가 가장 작은 에지라고 할 때, 빨간색 선 대신 파란색 선이 선택된다면, 파란색 선을 포함하는 Spanning Tree가 존재한다. 이 때, 파란 선 대신 빨간 선을 선택하면 가중치 합이 더 작은 Spanning Tree가 되므로, 빨간색 선을 추가하는 것은 안전하다.
구현
사이클이 생기지 않도록 Tree 구조를 이용해 구현한다.
1. Path compression (완벽한 path compression은 아니다)
2. Weighted Union
작은 트리를 Child로 만들면 더 적은 노드가 높이가 1씩 증가함 => 높이가 최대 logN이 된다.
class unionfind{
constructor(elements){
//초기화
this.count=elements.length;
this.parent={}
elements.forEach(e=>(this.parent[e]=e))
}
union(a,b)
{
var roota=this.findparent(a);
var rootb=this.findparent(b);
if(roota.root===rootb.root)
{
console.log('Alreday Connected')
return false;
}
if(roota.size>rootb.size)
{
this.parent[rootb.root]=roota.root
return true
}
else{
this.parent[roota.root]=rootb.root
return true
}
}
findparent(a)
{ var cnt=0;
var info={}
var b;
while(this.parent[a]!==a)
{
b=a;//for path compression
a=this.parent[a]
this.parent[b]=this.parent[a]
cnt++;
}
info['root']=a
info['size']=cnt
return info
}
}
class Kruskal{
constructor(nodes,edges){
//초기화
this.nodes = new unionfind(nodes);
this.edges = edges;
this.graph=[]
}
mst(){
while(this.edges.length>0)
{
this.findmin()
}
console.log(this.graph)
}
findmin(){
this.edges.sort(function(a,b){return a[2]-b[2]})
var minweight = this.edges.shift()
var result = this.nodes.union(minweight[0],minweight[1])
if(result)
{
this.graph.push(minweight)
}
}
}
var unionset=new unionfind(['A','B','C'])
unionset.union('A','B')
unionset.union('A','B')
unionset.union('C','A')
var nodes = ["A", "B", "C", "D", "E", "F", "G"];
var edges = [
["A", "B", 7], ["A", "D", 5],
["B", "C", 8], ["B", "D", 9], ["B", "E", 7],
["C", "E", 5],
["D", "E", 15], ["D", "F", 6],
["E", "F", 8], ["E", "G", 9],
["F", "G", 11]
];
var kruskal = new Kruskal(nodes,edges)
kruskal.mst()'ComputerScience > Algorithm' 카테고리의 다른 글
| dijkstra 알고리즘 (0) | 2020.06.09 |
|---|---|
| 최단경로 알고리즘 (0) | 2020.06.05 |
| 그래프 (0) | 2020.05.22 |
| [프로그래머스] 점프와 순간이동 (0) | 2020.05.21 |
| Hashing (0) | 2020.05.21 |