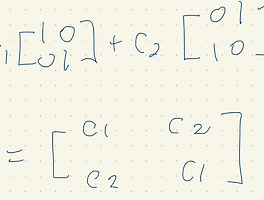행렬의 곱셈은 크게 열방향 또는 행방향으로 해석할 수 있다. 행렬에 벡터를 곱했을 때와 행렬을 곱했을 때의 성질들을 알아보자.
Multiplying by a vector
1.열방향 해석
A : m by n , b: n by 1
$Ab = b_1A_{*1}+b_2A_{*2}+....+b_nA_{*n}$
⇒ Combinations of columns of A
2. 행방향 해석
A : m by n, b: 1 by m
$bA = b_1A_{1*}+ b_2A_{2*}+...b_mA_{m*}$
⇒ Combinations of rows of A
Multiplying a matrix by another matrix
1. 열방향 해석
A: m by n , B : n by k
$(AB){*i}= AB{*i}=B_{1i}A_{*1}+B_{2i}A_{*2}+...+B_{ni}A_{*n}$
⇒ column combinations of A where coefficients taken from i-th column of B
2. 행방향 해석
$(AB){i*}=A_iB = A{i1}B_{1*}+A_{i2}B_{2*}+....+A_{in}B_{n*}$
⇒ row combinations of B where coefficients taken from i-th row of A
참고
www.statlect.com/matrix-algebra/matrix-multiplication-and-linear-combinations
Matrix multiplication and linear combinations
Matrix multiplication and linear combinations by Marco Taboga, PhD The product of two matrices can be seen as the result of taking linear combinations of their rows and columns. This way of interpreting matrix multiplication often helps to understand impor
www.statlect.com
'Math > Linear Algebra' 카테고리의 다른 글
| Vector Space와 Subspace (0) | 2021.01.16 |
|---|---|
| Row Equivalence (0) | 2021.01.08 |
| Basis (0) | 2021.01.06 |
| Permutation Matrix (0) | 2021.01.06 |
| Solvability of Ax=b (0) | 2021.01.04 |