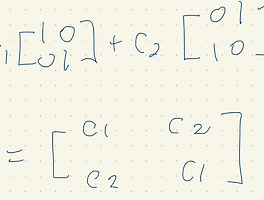Linear space
Linear space는 addition과 scalar multiplication 에 대해서 closed 되어있으면, linear space라고 한다. 즉 , linear combination에 대해 closed 되어 있으면 된다.
Uniqueness of representation in terms of basis
If $x_1,x_2,...,x_n$ are a basis for a linear space $S$, then the representation of a vector $s\in S$ in terms of the basis is unique. There exists one and only set of coefficients $a_1,a_2,..,a_n$ s.t $s=a_1x_1+...+a_nx_n$
Proof) Use proof of contradiction
Basis replacement theorem
Let $x_1,x_2,...,x_n$ be a basis for a linear space $S$. Let $s\in S$, then a new basis can be obtained by replacing one of the vectors $x_1,...,x_n$ with $s$.
Proof)
replace x_1 with s
-
show independence
-
show that is spans
Basis extension theorem
Let $x_1,...,x_k$ linear independent vectors belonging to a linear space $S$. Let $y_1,..,y_m$ a finite set of vectors that span $S$. Then we can form a basis by adjoining some elements of the spanning set to independent set.
Dimension of linear space
linear space의 차원은 linear space의 basis의 갯수로 정의된다.
Finite-dimensional space
어떤 linear space가 finite set of vectors로 span 가능하다면, finite dimensional이라고 한다.
Existence of basis
모든 finite dimensional linear space S는 적어도 1개의 basis를 가짐을 증명할 것이다.
-
위에서 finite dimensional space의 정의에 따라 linear space를 span하는 finite set of vectors V가 존재한다.
-
S로부터 하나의 원소 $s\neq 0$ 를 선택한다. I={s}는 Independent Set이다.
-
Basis Extension Theorem에 I와 V로 부터 Basis Set을 찾을 수 있다.
참고
'Math > Linear Algebra' 카테고리의 다른 글
| Vector Space와 Subspace (0) | 2021.01.16 |
|---|---|
| Row Equivalence (0) | 2021.01.08 |
| Permutation Matrix (0) | 2021.01.06 |
| Solvability of Ax=b (0) | 2021.01.04 |
| 행렬의 곱셈 법칙 (0) | 2020.12.31 |