Vector Space
vector space는 +(ADDITION)과 *(MULTIPLICATION)에 대해 닫혀(Closure)라면 Vector Space라고 한다.
Closure
Addition 에 대한 Closure란, $u$와 $v$가 $V$에 속하는 vector일 때, $u+v$도 $V$의 원소여야 한다.
마찬가지로 Multiplication에 대한 Closure란, $u$가 $V$에 속하는 vector일 때, $c\cdot u$ 도 $V$에 속해야된다. ($c$는 real number이다.)
보통 특정 Operation에 대해 closed 되어있다고 명시하고 Vector space는 Addition과 Multiplication에 대해 closed 되어 있다.
Subspace
$V$를 vector space라 하고 $W$를 $V$의 subset이라고 할 때, $W$가 $V$의 operation들에 대해 vector space를 형성하면 $W$는 $V$의 subspace이다. (closure under $W$)
Examples of non subspace
Subspace가 되지 않는 경우를 생각해보자.
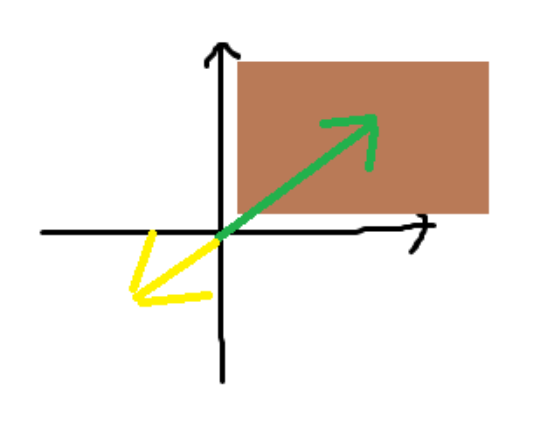
1사분면은 $R^2$의 subspace가 되지 않는데, 이는 초록색 벡터에 음수값을 곱하면 노란색 벡터가 되고, 이는 subspace에 포함되지 않기 때문이다. 즉, multiplication에 대해 닫혀 있지 않다.
Subspace의 성질
예를 들어 파란색 벡터로 만들어지는 line을 $R^2$의 subspace $L_1$이라하고 노란색 벡터로 만들어지는 subspace를 $L_2$라고 하자.

1. Subspace의 Union은 Subspace가 아닐 수 있다.
파란색 벡터와 노란색 벡터는 $R^2$ 공간을 모두 Span할 수 있다. 따라서 빨간색 벡터도 $L_1 \cup L_2$에 포함되어야 subspace가 될 수 있는데, 그렇지 않으므로 Subspace의 Union이 Subspace가 되지 않는 경우에 해당한다.
2. Subspace의 Intersection은 Subspace이다.
위의 예시에서 $L_1 \cap L_2= {0}$ . 즉 영벡터이다. 영벡터는 Subspace이므로 Intersection은 Subspace가 된다
General한 케이스에서도 Subspace의 Intersection이 Subspace가 됨을 쉽게 확인할 수 있다.
3. Subspace는 항상 영벡터를 포함한다
영벡터란 길이가 0인 벡터이다. 즉, 벡터의 모든 원소의 값이 0이다.
'Math > Linear Algebra' 카테고리의 다른 글
| Projections onto subspace (0) | 2021.02.02 |
|---|---|
| Orthogonal Vectors and Subspaces (0) | 2021.02.01 |
| Row Equivalence (0) | 2021.01.08 |
| Basis (0) | 2021.01.06 |
| Permutation Matrix (0) | 2021.01.06 |
